---

VI КОРНИ ЦЕЛОГО

Отрицательные и воображаемые числа

Теперь мы рискнём обратиться к алгебре. Использование в алгебре отрицательных и воображаемых чисел подтверждает четырёхчастную природу анализа и предоставляет дополнительный шанс использовать трёхчастный анализ. В этом случае мы снова должны предупредить, что намереваемся использовать концепции алгебры для целей, далеко выходящих за пределы обычного применения этих концепций, т. к. некоторые открытия алгебры привносят весомый вклад в наше исследование.

Эволюция математики пошла семимильными шагами после открытия возможности использования отрицательных чисел (отрицательных количеств). Если мы представим положительные числа как ряд, уходящий вправо от нуля, то слева от нуля будут отрицательные.
и т. д. ... -3, -2, -1, 0, +1, +2, +3… и т. д.

С помощью этого графика мы можем представить себе сложение, как движение вправо, а вычитание — как движение влево. Становится возможным вычитание большего числа из меньшего; к примеру, если мы вычтем 3 из 1, то получим -2, которое является реальным (хотя и отрицательным) числом.

Следующая важная концепция — воображаемые числа. Они были не открыты, а, скорее, случайно обнаружены. Математики пришли к выводу, что числа имеют корни, т. е. такие числа, которые, будучи помножены на самих себя, дают искомое число. Обнаружение отрицательных чисел и сопоставление их с корнями вызвало в научных кругах панику. Какими должны быть числа, умножение которых друг на друга дало бы число -1? Какое-то время ответа не было. Квадратный корень отрицательного числа было невозможно вычислить. Поэтому его и назвали воображаемым. Но когда Гаусс, прозванный «принцем математиков», открыл метод представления воображаемых чисел, вскоре нашлась и возможность для их применения. Сегодня ими пользуются наравне с реальными числами. Метод представления воображаемых чисел использует диаграмму Арганда, которая представляет собой цельность как окружность, а корни этой цельности — как участки окружности.

Вспомним, что ряд отрицательных и положительных чисел расходится в противоположные стороны из одной точки — нуля. Таким образом, квадратные корни целых чисел, +1 или -1, также могут быть выражены как противоположные концы линии, где в центре — ноль. Эту линию можно также представить как угол 180⁰, или диаметр.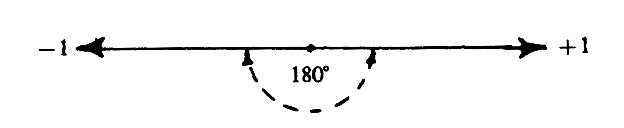

Гаусс развил первоначальное предположение и обрисовал квадратный корень из -1 как половину расстояния между +1 и -1, или как угол 90⁰ между линией от -1 до +1. Следовательно, если разделение целого на плюс и минус есть диаметр, или 180⁰, то второе разделение ведёт к появлению ещё одной оси, которая делит этот диаметр пополам, т. е. на угол 90⁰.

Таким образом, мы получаем две оси — горизонтальную, представляющую бесконечности положительных и отрицательных чисел, и вертикальную, представляющую бесконечности воображаемых положительных и отрицательных чисел. Получается обычная ось координат, где число, описываемое этой схемой и осями, есть число, имеющее реальную и воображаемую части.

Используя диаграмму Арганда (эту окружность с радиусом целого (радиус +1) на сложной системе координат), следующие корни целого (кубические корни, корни в четвёртой, пятой степенях и т. д.) мы находим простым делением окружности на три, пять и т. д. равных частей. Нахождение целого корня превращается в процесс вписывания многоугольников в окружность: треугольника для кубического корня, пятиугольника для корня в пятой степени и т. д. Корни становятся точками на окружности; их значения имеют реальную и воображаемую части, а высчитываются они, соответственно, по горизонтальной или вертикальной осям координат. Это означает, что они измеряются в терминах квадратных корней и корней в четвёртой степени.

Из этого мощного логического упрощения становится ясно, что анализ — процесс четырёхчастный. Любая ситуация может быть рассмотрена с точки зрения четырёх факторов или аспектов. Это не только лишний раз подтверждает Аристотилеву идею четырёх категорий, но и объясняет, почему квадратные уравнения (другими словами, «четырёхсторонние») так популярны в математике.

Но вывод о природе анализа как четырёхчастного по сути предполагает его работу в оба направления. Анализ же показывает и всеохватность четырёхчастного, и его ограниченность. А также то, что иногда суть опыта не поддаётся никакому анализу.

Находясь «внутри» геометрического метода, мы показали, что эти неаналитические факторы включают в себя тройственность, пяти нность, семи нность. Несмотря на то, что мы способны дать их аналитическое описание, — оно не способно раскрыть их истинную природу.

Кубические корни и трёхчастный оператор